|
El espectro que hemos obtenido está constituido opr líneas circulares centradas en el conductor. Esta estructura se hace más netamente visible en las proximidades de la corriente, lo que debemos atribuir a que allí las fuerzas que actúan son más intensas.
La planchuela suspendida, por su parte, se comporta igual que las limaduras, disponiéndose según las tangentes a las líneas del espectro, y por lo tanto normal al conductor.
Hemos establecido además que la brújula se orienta de igual forma que la planchuela, y que hay alguna relación entre el sentido de la corriente y la posición de la aguja, ya que al invertir aquella la aguja permuta la ubicación de sus extremos.
El concepto de campo
Cuando se trata de interacciones a distancia, la magnitud de las fuerzas que se manifiestan no depende sólo de los elementos que actúan, sino también de sus posiciones relativas.
La ley de gravitación universal establece que dos partículas materiales se atraen recíprocamente con fuerzas iguales y contrarias, cuyos módulos están dados por la expresión:
F1,2 = G m1 . m2 / d^2
en donde m1 y m2 son las masas respectivas, d es la distancia entre ellas, y G es una constante que depende del sistema de unidades adoptado.
Un artificio que permite simplificar el planteo y la resolución de problemas consiste en atribuir a los puntos del espacio la propiedad que tiene una masa (en nuestro caso la tierra, aunque podría tratarse de otro planeta o de un conjunto de planetas) de atraer a otras masas. Decimos entonces que existe un campo gravitatorio, porque en él se manifiestan fuerzas gravitatorias.
El razonamiento empleado es el siguiente: si m1 atrae a m2 ubicada en el punto A con una fuerza F de módulo:
F = G m1 . m2 / d^2 (2)
El cociente F/m2 resulta:
F / m2 = g = G m1 / d^2 (3)
donde g es el vector intensidad del campo gravitatorio, que nosotros ya conocemos como aceleración de la gravedad, y que tiene un valor próximo a los 10 m/s^2 en la superficie de la tierra, donde la fuerza gravitatoria se llama peso del cuerpo.
Cualquier otro cuerpo de masa m3 que se coloque en A estará sometido a una fuerza:
F = g . m3
Matemáticamente el procedimiento es inobjetable: suponemos que en cada punto del espacio que rodea a m1 (creadora del campo gravitatorio) existe un vector g (vector intensidad); la propiedad física de la atracción entre masas se ha transformado, mediante una abstracción, en una propiedad de los puntos del espacio que rodea a una de ellas, caracterizada por un vector g aplicado en cada punto. Dicho en otra forma: la presencia de una masa, exista o no otra masa con la cual pueda interactuar, confiere al espacio que la rodea una propiedad que antes no poseía.
Esta abstracción resulta útil para el tratamiento de problemas. Podemos decir que "en el punto A existe un vector g..." sin tener en cuenta qué lo origina, y tampoco si hay o no alguna masa en A.
Con los fenómenos eléctricos se procede de manera semejante: existe un hecho físico que es la atracción o la repulsión entre cargas, y a partir de ello se supone la aparición de un campo creado por una o por varias cargas. La expresión matemática es similar a la de gravitación:
F1,2 = k q1 . q2 / d^2 (4)
en la que q1 y q2 son las cargas eléctricas, d es la distancia entre ellas, y k es una constante que depende del sistema de unidades utilizado.
Por el mismo procedimiento se llega a:
F/q2 = E = k q1/d^2 (5)
donde E es el módulo del vector intensidad en un punto ubicado a una distancia d de q1.
Si el campo es creado por varias cargas E resulta de la composición de E1, E2, E3 ..... producidas por q1, q2, q3 ......
Mediante una nueva abstracción se crea el concepto de línea de fuerza, como la curva tangente a los vectores E, o como la trayectoria que seguiría una carga que se deje en libertad en el campo. Es decir, se ha elaborado todo un sistema para el análisis de los fenómenos eléctricos, utilizando conceptos abstractos deducidos a partir de los fenómenos naturales.
El campo magnético
Cuando comenzamos a tratar las interacciones entre cargas en movimiento hicimos referencia a la complejidad en la determinación de las fuerzas actuantes, dada la diversidad de variables que intervienen: magnitud de las cargas, velocidades (cada una de ellas definida por su módulo, su dirección y su sentido), y posiciones relativas de las cargas.
Para simplificar el tratamiento de los problemas magnéticos se ha recurrido a un criterio similar al adoptado para los fenómenos gravitatorios y eléctricos, es decir, al artificio de concebir un campo magnético creado por una carga o un conjunto de cargas en movimiento, y separadamente, al análisis de las fuerzas que, debido a la existencia de ese campo, actúan sobre otra carga u otro conjunto de cargas en movimiento.
Campo creado por una carga en movimiento
Supongamos una carga puntual positiva q1, que se desplaza por la recta m con una velocidad v1, y que pasa por el punto A en el instante considerado.
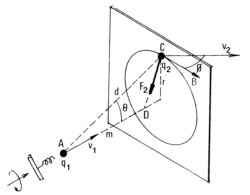
El vector intensidad B que q1 genera en un punto C cualquiera del espacio tiene las siguientes características:
- Su dirección es perpendicular al plano determinado por v1 y C. Es, en consecuencia, tangente a la circunsferencia de radio r, trazada sobre el plano perpendicular a v1 que contiene a C. Esa circunsferencia es una "línea de fuerza".
Definimos entonces como línea de fuerza magnética a aquella que es tangente a los vectores B del campo en todos sus puntos.
- El sentido de B se establece por la regla del tirabuzón: si éste avanza en el sentido de v1, su giro determina el sentido de B
- El módulo de B se determina por la expresión:
B = k` q1 v1 sen theta/d^2 (a)
donde d es la distancia del punto C a la carga, y k` es una constante que depende del sistema de unidades adoptado. (6)
Para un valor determinado de d, según esta fórmula, B es nulo para todos los puntos de la recta m (sen theta = 0) y toma su valor máximo para d perpendicular a v1 (sen theta = 1)
Acción del campo B sobre una carga en movimiento
Veamos ahora qué ocurre cuando por el punto C donde está aplicado B, pasa una carga positiva q2, con velocidad v2:
La fuerza F2 que actúa sobre q2 es normal al plano determinado por B y v2. Por ser F2 perpendicular a B, ocurre que F2 es coplanar con m, y su recta de acción la corta en algún punto (punto D en la figura). En el caso particular en que F2 y m resulten paralelas, esa intersección se produce en el infinito.
El sentido de F2 responde a la regla de la mano izquierda: si el dedo medio tiene el sentido de v2, y el índice el de B, el pulgar indica el de F2.
El módulo de F2 resulta de la expresión:
F2 = q2 . v2 . sen phi . B (7) (b)
en donde phi es el ángulo que forman los sentidos positivos de B y v2.
Según esta fórmula, F2 es nula para phi = 0 (B y v2 tienen la misma recta de acción), y toma su valor máximo para B y v2 perpendiculares.
Interacción entre ambas cargas
Hemos hecho el análisis del problema desglosando dos aspectos: la creación de B por q1, y la acción de B sobre q2. Si aplicamos las reglas y las fórmulas enunciadas en los párrafos anteriores al caso de dos cargas en movimiento, obtendremos iguales conclusiones que las expuestas al tratar el mismo tema como interacción entre cargas.
De las fórmulas (a) y (b) se obtiene el valor del módulo de F2:
F2 = k`/d^2 . q1 . v1 . sen theta . q2 . v2 . sen phi (8)
Por idéntico procedimiento se podrá determinar la fuerza F1 que q2 aplica a q1.
F1 y F2 son, por lo tanto, los elementos de la interacción entre ambas cargas. Salvo en casos muy particulares estas fuerzas no son colineales, ni paralelas, ni tienen igual módulo, contrariamente a lo que sucede con los fenómenos gravitatorios y eléctricos.
Esta modalidad de sustituir el tratamiento de los fenómenos magnéticos como interacción entre cargas por otro donde recurrimos al concepto de campo nos permite, por un lado, utilizar herramientas matemáticas para determinar con exactitud las fuerzas actuantes (9), y por el otro, aislar aquel aspecto del fenómeno que nos interese estudiar: la formación del campo, o la acción de ese campo sobre cargas en movimiento.
Campo creado por una corriente rectilínea
Supongamos una sucesión de cargas que se desplazan por una recta m con velocidad v.
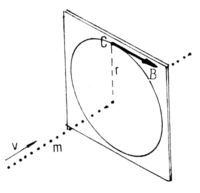
Los vectores intensidad que las cargas generan en un punto C coinciden en dirección y en sentido (regla del tirabuzón), aunque sus módulos difieren en función de la distancia entre C y cada carga. El campo B en ese punto, producido por el conjunto de cargas, será el resultante de los campos parciales, y responderá a la misma regla.
Puede decirse entonces, en forma general, que las líneas de fuerza del campo creado por una corriente rectilínea, son circunsferencias centradas en la corriente, y dispuestas en planos perpendiculares a la misma, con el sentido que establece la regla del tirabuzón.
Resulta aquí interesante destacar que la configuración del campo magnético deducida en nuestro razonamiento coincide con la disposición de las limaduras del espectro obtenido en nuestra experiencia. También hemos verificado que con ayuda de la brújula puede definirse el sentido de estas líneas.
El módulo de B se determina por métodos analíticos. Para un conductor de longitud infinita (en la práctica para un conductor mucho más largo que la distancia al punto considerado) la magnitud de B se determina por la fórmula:
B = k i/r (10)
donde k es una constante que depende del sistema de unidades utilizado, I es la intensidad de la corriente, y r la distancia al punto. B resulta entonces proporcional a la corriente, e inversamente proporcional a la distancia al punto considerado.
Acción del campo magnético sobre una corriente
En un párrafo anterior establecimos cómo actúa un campo B sobre una carga en movimiento.
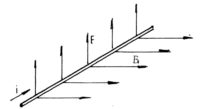
Si en lugar de una carga individual se trata de una corriente rectilínea el efecto será el mismo: sobre esta actuará un sistema de fuerzas, todas perpendiculares a B y a i en cada punto, siendo su sentido el establecido por la regla de la mano izquierda.
En el caso en que el campo no varía a lo largo del conductor, la fuerza total que actúa sobre él obedece a la misma regla, y su módulo será función lineal de B, de i y de la longitud del conductor:
F = i B l (11)
Cupla sobre una corriente cerrada en un campo homogéneo
Decimos que un campo es homogéneo cuando el vector intensidad tiene igual magnitud, dirección y sentido en todos sus puntos (es el caso del campo terrestre para zonas no muy extensas).
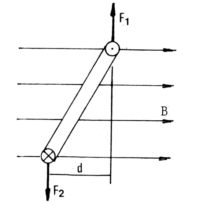
En la figura está representada una espira vista desde arriba, atravesando la superficie del papel. El símbolo X indica la intersección donde la corriente pasa hacia abajo O donde pasa hacia arriba.
Las fuerzas F1 y F2 tienen igual módulo, ya que la corriente es la misma en ambas ramas de la espira, y el campo B es constante. Son paralelas por su perpendicularidad con B y con la corriente, y de acuerdo con la regla de la mano izquierda, tienen sentidos opuestos. Constituyen entonces una cupla (M = F . d), que tiende a llevar la espira a una posición perpendicular al campo, en la que se dá una condición de equilibrio estable: las fuerzas tiran de la espira hacia afuera y no hay cupla, ya que d se hace igual a cero. (12)
Acción de un campo divergente sobre una corriente cerrada
Un campo es divergente cuando sus líneas se apartan unas de las otras en forma de abanico o como las plumas de un plumero.
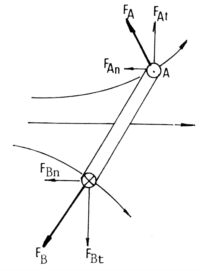
En la figura se ha representado un campo divergente, y en él una corriente cerrada que lo atraviesa. Las fuerzas FA y FB son perpendiculares a la corriente y a las líneas de fuerza en las intersecciones, y se las ha descompuesto según la paralela y la normal a la línea de fuerza que pasa aproximadamente por el centro de la espira.
Fan y Fbn la empujan hacia la zona de convergencia, y FAt y FBt la harán rotar hasta que ambas actúen según la misma recta.
El resultado es entonces que la espira es atraída hacia la región donde el campo es más intenso, adoptando una posición normal a sus líneas de fuerza.
Si la corriente circulara en sentido contrario al indicado en la figura, habría en el comienzo fuerzas de repulsión, pero la cupla produciría una rotación que la llevaría a la situación anterior.
Acción sobre una corriente cerrada del campo producido por una corriente rectilínea
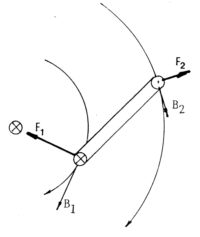
Este caso ya había sido estudiado como interacción entre corrientes.
Utilizando ahora el concepto de campo, llegamos a iguales conclusiones: siendo B1 mayor que B2, obtendremos F1 (atracción), mayor que F2 (repulsión). La disposición de ambas fuerzas nos indica que habrá una rotación (en sentido horario en la figura), que llevará a la espira al mismo plano que el conductor recto. Habrá finalmente una aproximación, por la prevalencia de F1.
Los tres casos analizados nos llevan a una conclusión de carácter general:
Una corriente cerrada que pueda girar y desplazarse libremente en un campo, se dispondrá normalmente a las líneas de fuerza, y se trasladará hacia la zona donde el campo es más intenso, o sea hacia donde se produce la convergencia.
Corrientes cerradas y átomos
Los electrones están dotados de dos clases de movimientos: se desplazan en órbitas alrededor del núcleo, y giran sobre sí mismos ("spin"). Ambos movimientos le confieren propiedades magnéticas: si se encuentran dentro de un campo, aparecen fuerzas que tienden a reorientar sus órbitas y sus ejes de rotación en la forma descripta en los párrafos anteriores.
Materiales magnéticos
En la mayoría de los elementos, su estructura interna no permite el cambio de orientación de las órbitas o del "spin" de sus electrones. Hay algunos pocos que sí responden, en mayor o menor medida, a las fuerzas magnéticas producidas por campos magnéticos externos: el hierro, el níquel y el cobalto.
De acuerdo con ello, en esos elementos (y en diversas aleaciones en que intervienen como componentes), los electrones en libertad para orientarse dispondrán sus órbitas y sus ejes de rotación en correspondencia con el campo que actúa sobre ellos. Si el campo es divergente, aparecerán también fuerzas que los empujarán (junto con los átomos a los que están vinculados) hacia la región donde la intensidad es mayor.
Como las corrientes cerradas y los "spin" de los electrones generan campos propios, tendremos un campo total, suma de estos y del campo externo que provocó su reorientación. En estas condiciones, ambos se refuerzan mutuamente. La componente que aportan los materiales magnéticos puede llegar a ser centenares o millares de veces superior al campo externo original.
El hecho de que las propiedades magnéticas que existen a nivel atómico en todos los elementos y sustancias no se ponga en evidencia debe atribuirse a que, no habiendo ordenamiento de los circuitos orbitales y de los "spin", el campo total que ellos producen tienen resultante nula en cualquier punto exterior al cuerpo de que se trate.
Los imanes permanentes
Hemos dicho que un material magnético es aquel que permite, en alguna medida, la orientación de las órbitas y de los "spin" de sus electrones, en correspondencia con un campo externo. Este fenómeno se llama "excitación magnética", y decimos que el material posee "magnetismo inducido". Si el campo externo desaparece, el material magnético, en general, conserva en parte el magnetismo inducido. Este magnetismo residual recibe el nombre de "histéresis" (memoria).
Un imán permanente es entonces una porción de material magnético que conserva en parte el ordenamiento inducido por un campo externo. Debido a esta estructura interna estable, un imán dispondrá su propio campo en correspondencia con cualquier campo externo dentro del cual se encuentre, si es libre de orientarse. La brújula es un imán permanente que puede girar sobre un eje, y su utilización nos permite determinar simultáneamente la dirección y el sentido de un campo magnético cualquiera.
Se ha establecido la convención de que las líneas de fuerza ingresan por el extremo S y salen por el extremo N de un imán.
Orientación de una limadura de hierro en un campo magnético
Supongamos una limadura de hierro en un campo magnético B. De acuerdo con nuestra hipótesis, se produciría una orientación de las órbitas y de los "spin" de algunos de los electrones del metal según ese campo externo (figura de la izquierda).
Ello no explicaría la rotación (que hemos verificado al producir espectros, y con la planchuela colgante que acomoda esas partículas en sentido longitudinal respecto al campo) (figura de la derecha).
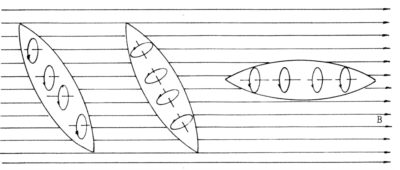
Debe suponerse que, luego de la excitación, se produce una reorientación en el interior de la masa metálica (donde los campos son muy intensos), y prevalece una interacción a nivel atómico, en la cual interviene ahora como variable la forma de la partícula. En nuestro caso se trata de cuerpos de mucha longitud respecto a su diámetro, y pareciera que la interacción interna impone una orientación longitudinal, como si todas las espiras se dispusieran haciendo coincidir sus ejes (figura central). Algo semejante hemos observado trabajando con dos espiras suspendidas, que se adosaron con una total correspondencia de sus perímetros.
Considerando una partícula como formadora de un campo, y a otra vecina como un sistema de corrientes cerradas, el encadenamiento de las limaduras se produce de la siguiente forma:
De los extremos de la primera emergen líneas de fuerza de un campo mucho más intenso que el del entorno.
Las corrientes cerradas de la segunda, por lo tanto, están sometidas a fuerzas que las llevan hacia ese extremo, donde las líneas de fuerza convergen, disponiendo sus órbitas normales a ellas.
Dicho de otra manera, las partículas tienden a pegarse por sus extremos y conservan su alineamiento con el campo externo.
Debe advertirse que la presencia de material magnético modifica en alguna medida la configuración del campo externo, debido a su propio aporte. No obstante, por la baja densidad de las limaduras, podemos admitir que esa influencia es puntual y de poca relevancia, y que las líneas del campo que se investiga coinciden con bastante exactitud con las líneas del espectro.
En qué forma una masa importante de material magnético modifica el espectro, podrá verificarse formando un espectro de limaduras y colocando debajo de la superficie de ensayo un trozo de hierro de buen tamaño (por ejemplo un bulón).
Si nuestras conclusiones son acertadas respecto a la coincidencia entre las líneas de fuerza magnética y las líneas de limaduras de los espectros, disponemos de un medio sumamente eficaz para visualizar el campo, cualquiera sea la configuración geométrica del conductor que transporta la corriente. Todas las conclusiones que obtengamos observando espectros se basarán precisamente en ese supuesto.
Anterior Siguiente
|
DESDE 1996
Las guías constructivas y de trabajos prácticos aquí presentadas fueron creadas por el
Ing. Agustín J. Frascino (QEPD 15-II-08) con la ayuda del Ing. Sergio San Román con el objeto de fomentar el trabajo experimental en la
Enseñanza de la Física, aún en los casos en que la escasez de recursos económicos parecerían
forzar a docentes y alumnos a contentarse con clases de tiza y pizarrón.